Archive December » Andrew Alvarez

Archive for December, 2013

Part 1: Integration, Inertia, and Quaternions

This is going to be the start of a series of posts on interactive motion dynamics as they apply to physics engines. The goal is that by reading through all of these posts someone would be able to understand and implement a full-fledged 3D physics engine and, more importantly, actually understand what they are doing.

F = m * a and T = I * α

Like everything in physics, we start with F = m*a and T = I * α. Force equals mass times acceleration. Torque equals inertia tensor (more on this later) times angular acceleration. The fundamental way that things move around in our system will be based off of these two equations. For our system we are going to be using rigid bodies of uniform density. The reason behind this choice is for simplicity of simulation. In reality, there is no such thing as a “rigid body”, objects will always have some bit of give, some amount of deformation. But modeling this real-time is actually quite hard. So, let’s not. But to start, let’s just create a class called RigidBody that has mass, acceleration, an inertia tensor, and an angular acceleration because that seems to be the obvious thing to do. We also need position and orientation.

class RigidBody
{
  real m_mass;
  Vec3 m_acceleration;
  Mat4 m_inertiaTensor;
  Vec3 m_angularAcceleration;

  Vec3 m_position;
  Quat m_orientation;
};

So, we actually don’t want to store the mass or inertia tensor. What we want to store is the inverse of these values. This is because we are wanting to get the acceleration/angular acceleration based on the forces/torques that are being applied and the mass/inertia tensor of the object. Also, since we are determining what the acceleration/angular acceleration is, we don’t need to actually store it in the class since it gets recalculated every frame based on the accumulated forces/torques being applied. But, this does mean that we need to store all the forces/torques that have been accumulated over the previous frame.

class RigidBody
{
  real m_inverseMass;
  Mat4 m_inverseInertiaTensor;

  Vec3 m_force;
  Vec3 m_torque;

  Vec3 m_position;
  Quat m_orientation;
};

Quick little aside. I prefer to typedef my data types. So, a real is either a float or a double, a Vec3 is a 3D vector, a Mat4 is a 4 by 4 matrix, and a Quat is a quaternion. This is done to allow changing precision or the math classes used for the engine easily, provided that the new math classes conform to the same interface that the physics engine is expecting. I also haven’t really explained what a quaternion is. The actual answer to what a quaternion is would take quite a bit of time to explain, but all that is required knowledge for now is that normalized quaternions map to the unit sphere in 3D. This allows for an easy and compact way to store orientation data about objects. I’m assuming some familiarity with linear algebra so I’m not going to explain anything about vectors or matrices. I’ll actually explain a lot more in-depth about what these are and how to use them when we get there. Anyway, back to the matter at hand. So, inertia tensors can be a bit complicated. Essentially though, they are the rotational equivalent to mass. Conceptually, calculating them isn’t too terribly difficult to grasp. Since we are in 3D, we have 3 principle Cartesian axes that we can rotate around. What we need to find is how resistant an object is when it comes to rotating around one of these axes. I’m going to skip some of the derivation of this formula for everyone’s sake, but the main idea behind the derivation actually makes quite a bit of sense.

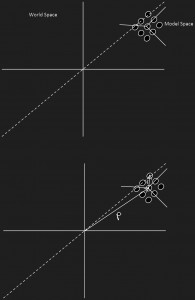
Imagine you have an object made up of 1000 particles of uniform mass that may never move relative to its neighboring particle. However, as long as these particles stay relatively the same distance to each other, they may move around. So, if the object is wildly spinning and moving around, each of those particles are moving in world space but relative to the object’s other particles they are not moving. Well, if we average the position of all those particles we have the object’s center of mass since we assume uniform density. Each of these particles, $\alpha$ , also has a kinetic energy based on it’s translational movement through the world.

$T=\frac{1}{2}m_\alpha v_\alpha^2$

So, as previously stated our particle, $\alpha$ , is moving around in the world. But it’s movement is constrained by the other particles. Its position must remain relative to the others. This means that it’s radial distance from the center of mass, $r$ , is going to be constant. So, if you want to know why this following equation is the way it is, it’s because of the movement of reference frames. Right now we are actually working with two, model space and world space. I kept saying that all the particles don’t move relative to each other and have a center of mass. Well, none of the particles move in model space and the origin of model space is the center of mass of the object.

$P$ is the position vector of the center of mass (which is the origin of the model space reference frame) and $r$ is position vector of the particle in model space. Velocity is the derivative of position. Just like acceleration is the derivative of velocity. Well, since we are trying to find $v_\alpha$ , we obviously need to take the movement of the model space reference frame into account (the origin of which we are treating as our center of mass). Let’s call this $v_w$ . We now need to find the velocity caused by the rotation of the model space reference frame in world space. The rotation of the model space reference frame in world space we will call $\omega$ . The rotation of this particle relative to world space is found by $\omega\times r$ . This means our total velocity is

$v_\alpha=v_w+\omega\times r$

Now, we can determine the total energy for the 1000 particle object by taking the sum of all particles’ energy.

$T=\frac{1}{2}\sum_{\alpha}m_\alpha(v_w+\omega\times r_\alpha)^2$

Expanding out and such looks like…

$T=\frac{1}{2}\sum_{\alpha}m_\alpha(v_w+\omega\times r_\alpha)^2$

$T=\frac{1}{2}\sum_{\alpha}m_\alpha v_w^2+\sum_{\alpha}m_\alpha v_w\cdot(\omega\times r_\alpha)+\frac{1}{2}\sum_{\alpha}m_\alpha*(\omega\times r_\alpha)^2$

Well, that first term is clearly translational energy for the system. The last term is rotational energy. The middle term, well, it’s not important. In fact, for our purposes it goes away completely. The last term is what we are working with right now because we’re trying to figure out what inertia tensors are. After some serious algebra (none of which I’m going to show) we end up with the following equation:

$T_{rot}=\frac{1}{2}\sum_{i,j}\omega_i\omega_j\sum_\alpha m_\alpha*(\delta_{ij}\sum_kx_{\alpha,k}^2-x_{\alpha,i}x_{\alpha,j})$

Where $r_\alpha=(x_{\alpha,1},x_{\alpha,2},x_{\alpha,3})$ .

Integrals are sort of like the continuous version of a discrete summation and since we aren’t actually dealing with a bunch of particles in our simulation it makes more sense to turn the summation into an integral. Also, since we’re trying to find the rotational analogue to mass, we will get rid of $\frac{1}{2}\sum_{i,j}\omega_i\omega_j$ , which is really just $\frac{1}{2}\omega^2$ . Calculating the moment of inertia around an axis is simply done by taking the following integral now:

$\int_V\rho(r)*(\delta_{ij}\sum_{k}x_k^2 - x_ix_j) \partial v$

We can actually make a few assumptions to make things easier. $\rho(r)$ is the density of the object with respect to distance from the center of mass. Since we are working with objects of uniform density, this is a constant value and may go out of the integral. This also means we get rid of r, seeing as density is no longer a function of the distance from the center of mass.

$\rho\int_V(\delta_{ij}\sum_{k}x_k^2 - x_ix_j) \partial v$

Neat. Let’s keep assuming and simplifying. $\delta_{ij}$ is what is called the Kronecker delta. It’s probably my least favorite math symbol. All it means, in this case, is that if $i=j$ then $\delta=1$ , otherwise $\delta=0$ . So, what do $i$ and $j$ mean here? Well, like I said before, we are trying to calculate an inertia tensor, which looks like a matrix. It’s not though! It’s a tensor. While they are represented the same way, the operations you perform on them are a bit different. But we will get to that later, just keep that in mind for now. So, $i$ and $j$ represent the row and column of our tensor, $I$ , respectively. Also, since we are working in 3D, $\sum_{k}x_k^2$ always translates to $x_1^2+x_2^2+x_3^2$ , or $x^2+y^2+z^2$ , if you prefer to see it that way. The integration is essentially a volume integration, so in 3D you’re actually taking a triple integral along the x, y, and z axis. This thing also happens where, if your origin is the center of mass and you have some kind of regular polygon and your axes have symmetry along the negative and positive parts, the only entries in your inertia tensor that aren’t zero are the diagonal indices. This is what we actually want to calculate. So, make sure to pick your origin and axes appropriately.

Also, since I’m sure your don’t actually want to go through calculating the inertia tensor for a box which has been done millions of times by this point, check this Wikipedia link to see a list of common inertia tensors.

Anyway, back to the original topic. Change in position is velocity. Change in orientation is angular velocity. So, let’s add those to our class.

class RigidBody
{
  real m_inverseMass;
  Mat4 m_inverseInertiaTensor;

  Vec3 m_force;
  Vec3 m_torque;

  Vec3 m_velocity;
  Vec3 m_angularVelocity;

  Vec3 m_position;
  Quat m_orientation;
};

Side-note: I avoid using the word “rotation” pretty much anywhere in my code because it actually is quite an ambiguous word seeing as it can refer to either orientation or angular velocity. Well, now that we have an appropriate class, let’s make things move by integrating some forces. Just like the derivative of position is velocity and the derivative of velocity is acceleration, the integral of acceleration is velocity and the integral of velocity is position. We use our accumulated forces to calculate acceleration, then we use that acceleration to modify our velocity, then we use that velocity to set our new position. This process is called “Integration”.

Integration

There are actually a bunch of different ways to perform this operation. I want to say that, for rigid body simulations in real-time, the method known as “Semi-Implicit Euler” is almost universally accepted as the best method to use. The idea behind this method is to update the velocity based on the forces/acceleration of the previous frame, then use that velocity to perform collision resolution by applying impulses to colliding objects (or resolve velocity constraints, but that part is pretty far down the road), and then use that new velocity to update the position.

void RigidBody::IntegrateVelocity(real dt)
{
  Vec3 acceleration = m_force * m_inverseMass;
  Vec3 angularAcceleration = m_torque * m_inverseWorldInertiaTensor;

  m_velocity += acceleration * dt;
  m_angularVelocity += angularAcceleration * dt;
}

void RigidBody::IntegratePosition(real dt)
{
  m_position += m_velocity * dt;
  m_orientation *= Quat(m_angularVelocity * dt);
}

You might have noticed a new member variable appear, m_inverseWorldInertiaTensor. This is because the inertia tensor we learned how to calculate earlier is actually only the correct tensor for that object in model space. We need to transform that tensor into world space for it to give correct results. Remember how I said earlier that tensors work a little bit different that matrices even though they look pretty much the same? Well, here’s the main difference: a matrix’s basis vectors are either its rows or columns (depending on if you work row-major or column-major, I work row-major) while a tensor’s basis vectors are both its rows and columns. This means that when transforming the inertia tensor from model space to world space we have to multiply it by the orientation and the inverse orientation.

void RigidBody::CalculateWorldTensor(void)
{
  m_inverseWorldInertiaTensor = m_orientation * m_inverseInertiaTensor * m_orientation.Inverse();
}

There are a few other things we will need to take care of during integration. But we’re only going to address one of these things now. In the real world (except the vacuum of space), there is drag caused by friction with air. We don’t want to actually simulate this phenomenon because it would be rather slow. So, instead we’re just going to apply a damping factor to the velocity being applied so it slowly decreases over time.

Another thing you may be wondering is how the whole orientation part of this works. Well, now it’s time to look at what quaternions are.

Quaternions

You may have heard someone say in the past, “Quaternions are orientations.” Well, they’re wrong. Quaternions are not orientations. They can, however, represent an orientation in $\mathbb{R}^3$ if the quaternion is normalized. But before we get to why that is, how that works, and how to use quaternions, let’s look at some of the basic concepts involved in quaternion math.

Probably the biggest thing that throws people off is that quaternions contain both real and imaginary numbers. In fact, a quaternion looks a lot like a 4D vector in representation except that instead of x, y, and z we use i, j, and k. That’s because these axes are actually imaginary. Yes, imaginary. That is the actual, technical, mathematical term. Anyway, while a 4D vector has the 4th axis often being referred to as w, a quaternion’s 4th axis is generally called r. This is actually the only real number in a quaternion, all the others are imaginary.

Since we have one real number and three numbers along imaginary axes, it is appropriate to consider a quaternion to be made up of a scalar and a vector:

$q=a+bi+cj+dk=a+\vec{v}$

So, without getting into the reasons why this works the way it does, creating a quaternion from an axis of rotation and an angle is pretty simple. It’s just the following formula:

$q=(r,i,j,k)=(\sin{\theta},x*\cos{\theta},y*\cos{\theta},z*\cos{\theta})$

$\theta$ represents the rotation of an object around the axis $(x,y,z)$ . This is a pretty nifty formula and it can be used to construct a quaternion from the Euler angles used to represent the angular velocity of our objects. A pretty simple way to do this is to just construct three quaternions, one facing in each the x, y, and z directions and then multiply those quaternions together. Well, this is the next step, quaternion multiplication. It’s actually pretty easy to figure out, so let’s do that. We will start with two quaternions, $p$ and $q$ .

$pq=(a_1,b_1i,c_1j,d_1k)\cdot(a_2,b_2i,c_2j,d_2k)=(a_1+\vec{v}_1)\cdot(a_2+\vec{v}_2)$

Well, multiplication in quaternion space operates a tiny bit different than in a normal vector space. But that isn’t because the actual multiplication process is different. It’s because of some properties of quaternion space. You see, the axes are imaginary and imaginary numbers, when multiplied together, are negative (because $\sqrt{-1}^2=-1$ ). In other words

$i^2=j^2=k^2=ijk=-1$

So, keeping that property in mind, we expand and do some algebra to find that

$(a_1+\vec{v}_1)\cdot(a_2+\vec{v}_2)=(a_1a_2-\vec{v}_1\cdot\vec{v}_2)+a_1\vec{v}_2+a_2\vec{v}_1+\vec{v}_1\times\vec{v}_2$

I recommend you go through the process of deriving this yourself. I’ll post a more in-depth look at quaternions some time in the future and go over the fundamentals of them and how they work. But for now, this knowledge should be enough to get by.

Next Post…

Well, hopefully this was enough to grasp how objects move about in a 3D physics engine. In the next part, I’m going to go over some basic concepts used in collision detection such as the Minkowski Difference, Configuration Space, and the two most commonly used collision detection algorithms.